이 글은 개인의 학습을 목적으로 정리한 글입니다. 이점 참고하고 읽어주세요 ;)

이번 포스팅에서 다룰 것은 N-queens라는 문제입니다. N-queens 문제는 아래의 그림과 같이 N * N개로 나뉜 공간에서 N개의 점들이 단 한 점도 동일 선상 위에 놓이지 않게 배열하는 문제입니다. 마치 체스에서 직선과 대각선 모두 이동할 수 있는 퀸에게 잡히지 않게 말들을 배열하는 것에서 그 이름을 따왔을 것이라고 생각합니다.

이 포스팅에서는 N-queens 문제를 상태 공간 트리에서 Backtracking을 통해 해결하는 방법에 대해 알아볼 것입니다.
우선 상태 공간 트리란 가능한 모든 경우의 수들을 노드를 통해 연결한 개념적 그래프를 의미합니다. 가능한 모든 경우의 수를 다루고 있기 때문에 우리가 찾는 해 역시 트리의 한 노드로 연결되어있고 그렇기에 트리의 노드들을 방문하다 보면 해는 반드시 구할 수밖에 없습니다.

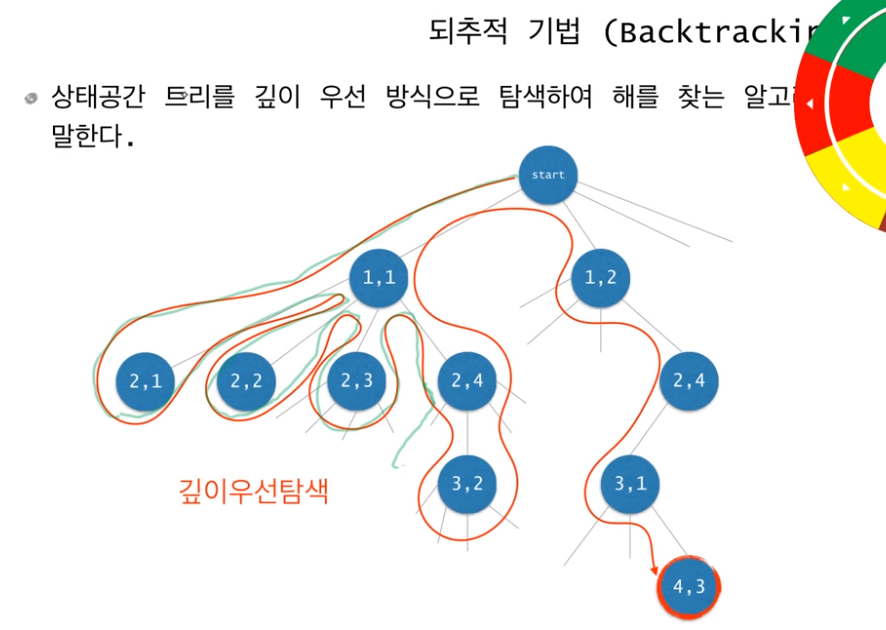
상태 공간 트리의 노드들을 한 번씩 방문하며 해를 찾는 과정이지만, 그렇다고 모든 경우의 노드들을 끝까지 방문한다는 말은 아닙니다. 해를 만족시키는 조건을 if문 혹은 while문을 통해 설정하고, 이 조건을 계속 확인하며 노드들을 방문합니다. 이러한 과정을 Backtracking 기법이라고 합니다.

N-Queens 역시 Recursion을 이용합니다. Recursion의 핵심이라면 자신의 상태로부터 하위 상태를 다시 호출하는 구조를 반복하여 답을 찾아가는 것입니다.
N-Queens의 답을 찾는 함수인 queens 함수는 자신이 속한 상태가 답이 될 수 있는 promising한 상태가 아니라면 이전의 상태로 돌아가는 back-tracking을 통해 다른 답을 찾고, 최종 해답 상태라면 success를, failure도 success도 아닌 상태 즉, 이전 줄의 말들과 겹치지 않는 상태라면 자신보다 아랫줄에서의 queen 함수를 호출하여 다음 줄의 답을 찾고 이런 구조를 반복합니다.


체스판은 2차원이지만, 말의 위치를 나타내는 배열은 int[] cols는 굳이 2차원이 아닌 1차원 배열로 만들어도 상관 없습니다. 배열의 index는 체스판의 줄, index에 해당하는 값은 멤버를 말이 해당 줄에서 몇 번째 위치에 있는지로 나타내면 됩니다.


N * N 길이의 체스판이기 때문에 말이 위치한 줄을 나타내는 level이 N과 같아졌다는 건 체스의 말이 체스판의 끝에 도달했다는 말입니다. 때문에 level==N이면 함수가 종료됩니다.
자식 노드에 방문한 뒤 다시 queens 함수를 recursion으로 호출하여 유효성을 검증하며 다음 Level의 노드로 넘어가는 구조로 n-Queens 문제를 해결합니다.



public class nQueens {
static int N=8;
static int[] cols = new int[N+1];
static boolean promising(int level)
{
for(int i=1; i<level; i++)
{
if(cols[i]==cols[level]) // 기존까지 놓인 말들이 level줄의 말과 겹치는 동선인지 확인
return false;
else if(level-i==Math.abs(cols[level]-cols[i])) // 두 말이 동일한 대각선인지 확인
return false;
}
return true;
}
static boolean queens(int level) {
if (!promising(level))
return false;
else if (level == N) {
for (int i = 0; i <= N; i++)
System.out.println("(" + i + ", " + cols[i] + ")");
return true;
}
return false;
}
}'Information Technology > Algorithms' 카테고리의 다른 글
| [JAVA] 기본적인 정렬 알고리즘 (0) | 2020.01.31 |
|---|---|
| [JAVA] 멱집합 (0) | 2020.01.22 |
| [JAVA] Recursion 응용: Counting Cells in a Blob (0) | 2020.01.16 |
| [JAVA] Recursion 응용: 미로찾기 (0) | 2020.01.16 |
| [JAVA] Recursion 설계 (0) | 2020.01.10 |



